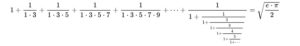Biography of a great Indian mathematician Srinivasan Ramanujan

Srinivasa Ramanujan Iyengar was a great Indian mathematician. He is counted among the greatest mathematical thinkers of modern times. He did not get any special training in mathematics, yet he made significant contributions in the fields of analysis and number theory. He made substantial contributions to the analytical theory of numbers and worked on elliptic functions, continued fractions, and infinite series.

About Srinivasan Ramanujan:

Ramanujan was born on December 22, 1887, in the village of Erode, in Coimbatore, in the southern part of India. He was born in a traditional Brahmin family. His mother’s name was Komalathammal and his father’s name was Srinivas Ayyangar.

His childhood was mainly spent in Kumbakonam (Town in Tamil Nadu), which is known for its famous ancient temples. In childhood, Ramanujan’s intellectual development was not the same as normal children. He could not even learn to speak till the age of three. When Ramanujan did not begin to speak when he was such a big age, everyone was worried that it was not dumb.

Education of Ramanujan:

When he entered school, he never felt in traditional education. Ramanujan received the highest marks in the whole district in the primary examination at the age of ten years and reached the high school for further education.

Ramanujan liked to ask questions. His question teachers sometimes seemed very distraught. Like, who was the first man in the world? What is the distance between the earth and the clouds? Ramanujan’s behavior was very sweet. According to his classmates, his behavior was so sweet that no one could be angry with him. His talent at school started influencing other students and teachers. He had only read college-level mathematics during school hours. Once the school’s principal also said that the standards of examination in the school are not applicable to Ramanujan. After passing the high school exam, he got Subramaniam Scholarship to get good marks in Mathematics and English and also got admission for the college education.

The craziness of Ramanujan’s for mathematics was so much, that he did not pay attention to other subjects. Even he was used to solving math problems in history and biology classes. Consequently, in Eleventh Class examination, he failed in all other subjects except mathematics and as a result, he stopped receiving a scholarship. Nobody was able to obtain the financial status of the home and the above scholarship. It was a difficult time for Ramanujan. To improve the condition of the house, he also did some mathematical tuitions and account books. After some time, in 1907, Ramanujan again gave the class 12th private examination and failed.

When Srinivasa Ramanujan was studying in the matriculation class, he found a text of mathematics from the local college library. ‘A Synopsis of Elementary Results in Pure and Applied Mathematics‘ was authored by ‘George S.’ George (Shoobridge Carr). ‘Ramanujan, George S. After reading the book written on the results of the mathematics of the work, and influenced by this book, he started working on mathematics himself.

By 1904 Ramanujan had begun to undertake deep research. He investigated the series ∑(¹/_n) and calculated Euler’s constant to 15 decimal places. He began to study the Bernoulli numbers, although this was entirely his own independent discovery.

Professor Hardy’s Cambridge Invitation:

Due to some personal reasons and lack of money, Ramanujan rejected Professor Hardy’s invitation to Cambridge. Professor Hardy disappointed with this, but he decided to call Ramanujan in any way. Gradually, Professor Hardy agreed to Ramanujan to come to Cambridge. With the efforts of Professor Hardy, Ramanujan got financial help to go to Cambridge. Before going to England, Ramanujan had written more than 3000 new sources of mathematics in his notebook. This journey of England brought revolutionary change in his life. He published a high-profile paper with Professor Hardy. Due to his special research, he was awarded a BA by Cambridge University. Also got the title of but the climate and lifestyle of them were not favorable and their health remained poor. Doctors described it as TB disease. At that time there was no medicine for tuberculosis and the patient had to live in a sanatorium. Ramanujan had to stay there for a few days. At this time there used to be new ideas in mathematical formulas.

1729 known as the Ramanujan number:

This story is very famous among mathematicians. 1729 is sometimes called the “Hardy-Ramanujan number”.

There are two ways to say that 1729 is the sum of two cubes. 1x1x1=1; 12x12x12=1728. So 1+1728=1729 But also: 9x9x9=729; 10x10x10=1000. So 729+1000=1729 There are other numbers that can be shown to be the sum of two cubes in more than one way, but 1729 is the smallest of them.

‘Ramanujan number’ is the natural number that can be represented by the sum of two cubes of two numbers in two different ways.

1729=1³+12³=9³+10³

Important work by Srinivasan Ramanujan:

Earlier, he used to write a new formula or mathematical form before but did not pay much attention to it. When asked about this, he used to say that this formula has received him from the grace of Namagiri Devi. Ramanujan’s beliefs about spirituality were so deep that he considered any of his work done in the field of mathematics as part of spirituality. They did not only believe in religion and spirituality but also presented it logically. They used to say that “there is no point in mathematical formula for me that I do not get spiritual ideas.”

Ramanujan develops his mathematical ideas and began to pose problems and solve problems in the Journal of the Indian Mathematical Society.

He developed relations between elliptic modular equations in 1910.
Research paper on Bernoulli numbers in 1911.
He wrote a high-level paper on the mock theta function. This function, used by Ramanujan, is used not only in mathematics but also for understanding cancer in medical science.

Formula:

Ramanujan projected the following formula-

The advantage of this formula is that it expresses the relationship between the two most famous determinants of mathematics (‘pie’ and ‘e’) through an infinite continuous fraction. For Pi, he also gave a second formula (in the year 1910)

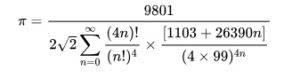The death of Ramanujan:

Their health has become a cause for concern for all and even now doctors gave the answer. At last, the clock of Ramanujan’s departure came In the early hours of April 26, 1920, he became unconscious and in the afternoon he left life. Ramanujan was only 33 years old at this time. His untimely death was irreparable damage to the mathematical world. Whoever heard the news of the death of Ramanujan all over the country, became stunned.

Exam News and Updates

Biography of Srinivasan Ramanujan